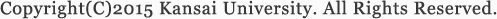さまざまな問題を解決するための数学的構成能力、
論理的思考能力を養う。
-
【研究室】 確率解析
【研究分野】 確率解析学上村 稔大 教授
-
【研究室】 幾何解析
【研究分野】 幾何解析庄田 敏宏 教授
-
【研究室】 確率論
【研究分野】 確率論竹田 雅好 教授
-
【研究室】 計算科学
【研究分野】 計算科学寺本 央 教授
-
【研究室】 微分幾何学
【研究分野】 微分幾何学藤岡 敦 教授
-
【研究室】 整数論
【研究分野】 整数論村林 直樹 教授
-
【研究室】 代数学
【研究分野】 可換代数柳川 浩二 教授
-
【研究室】 表現論
【研究分野】 表現論和久井 道久 教授
-
【研究室】 統計学
【研究分野】 数理統計学上原 悠槙 准教授
-
【研究室】 可積分系
【研究分野】 可積分系神吉 雅崇 准教授
-
【研究室】 数理モデル
【研究分野】 確率数値解析田口 大 准教授
【研究分野】 確率解析学
さいころを振り続けると1の目が出る確率が1/6 になるのはなぜでしょう?また、コインを投げ続けると表の出る確率も 1/2 となるのはなぜでしょう? この疑問に答えるのが確率論です。このような不規則な現象の系列から規則性を見付け出す研究を行います。

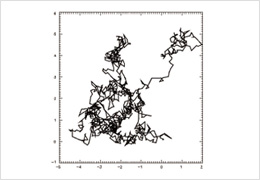
2次元ブラウン運動の軌跡
【研究分野】 幾何解析
様々な自然現象の原理を数式で記述することが主な目的です。その現象を考察する舞台として多様体という便利な空間を扱い、その自然現象を多様体上の何らかの偏微分方程式の解によって記述します。それらの情報から得られる幾何学的量を研究しております。


トーラスから2点を除いた曲面に見えますか?
【研究室】 確率論
竹田 雅好 教授
mtakeda![]()
【研究分野】 確率論
ランダムな時間発展のモデルのなかに、「現在の情報が分かっていれば、未来の確率情報は過去の情報に依らない」という性質を持つマルコフ過程と呼ばれるクラスがあります。マルコフ過程から定義される様々な確率量を解析する研究を行っています。
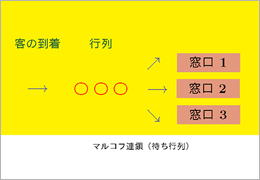
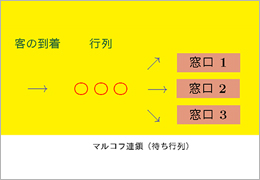
マルコフ連鎖(待ち行列)
【研究室】 計算科学
寺本 央 教授
teramoto![]()
【研究分野】 計算科学
グレブナー基底に代表される計算代数のアルゴリズムの開発およびその特異点論、ハミルトン力学系、化学反応動力学、プログラム検証等への応用


新規化学反応機構「反応座標スイッチング」の概念図 (Phys. Rev. Lett. 115, 093003 (2015))
【研究分野】 微分幾何学
世の中のさまざまな図形やそれらを数学的に抽象化したものの中から、特に幾何学的に興味深いものに注目し、それらがなぜそのような形をしているのか、あるいは、どのような性質を持っているのか、といったことを主として微分法を用いて研究しています。

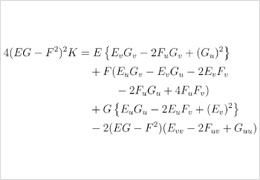
天才ガウスもびっくり!!
【研究分野】 整数論
楕円曲線やその高次元化であるアーベル多様体に関する研究を行っています。y²=「xの3次式」という式で定義される代数曲線を楕円曲線と言います。これは、ゼータ関数を通して、保型形式と呼ばれる対称性を持った関数と深い関係を持っています。また、情報セキュリティに関する暗号理論との関連でも研究されています。
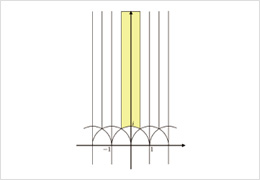
SL(Z)の基本領域。境界を貼り合わせることにより、1次元アーベル多様体(=楕円曲線)のモジュライ空間となる。
【研究分野】 可換代数
「代数学」は、数学の一分野ですが、物事をその「構造」から捉える姿勢が強いものです。広大な領域ですが、本研究室では、可換環の組合せ論的側面を中心に、独自の手法も用いて研究しています。「マトロイド」等、一部の応用数学とも関連します。
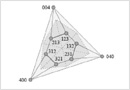
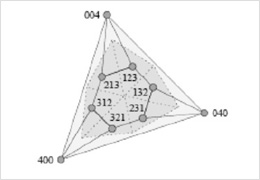
Miller-Sturmfels著『Combinatorial Commutative Algebra』より。
【研究分野】 表現論
円周、線分、球面、多面体などの図形をゴムや粘土の柔らかい素材で出来ていると思って伸縮させて研究する数学の分野にトポロジーがあります。当研究室では、トポロジーをベクトルや多項式などの計算に反映させて研究しています。
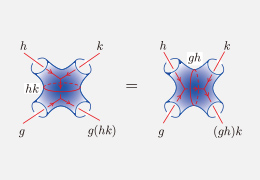
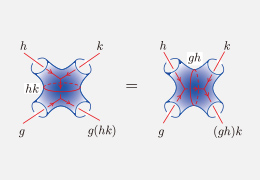
2コサイクル(2cocycle)
【研究分野】 数理統計学
株価や動物の行動といった時系列データから情報を抽出するために用いられる、確率微分方程式モデルの統計手法を中心に研究しています。また、確率微分方程式モデルのシミュレーションのための乱数生成手法の研究、およびソフトウェア開発も行なっています。
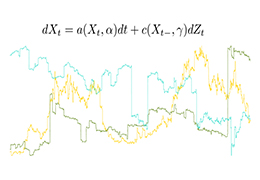
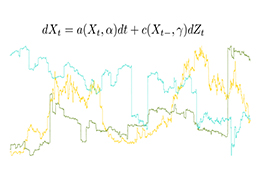
確率微分方程式モデルと解過程のサンプルパス
【研究分野】 可積分系
普通ならうまく解けないはずの方程式が、なぜか厳密に解ける現象を調べる分野を可積分系といい、数学的なしくみを研究しています。可積分系はコンピュータシミュレーションとも相性がよく、生物学や工学など他分野への応用も注目されています。


離散KdV方程式とそのソリトン解
【研究室】 数理モデル
田口 大 准教授
taguchi![]()
【研究分野】 確率数値解析
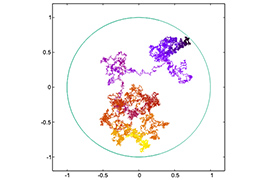
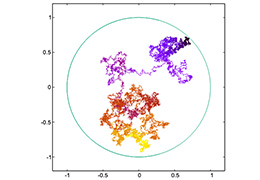
確率過程のシミュレーション