さまざま問題を解決するための数学的構成能力、論理的思考能力を養う。
急激な変化と発展を遂げる現代社会では、さまざまな分野で数学的思考に基づいて、現象の本質の解析と数理的定式化のできる人材に対するニーズが、非常に高まっています。数学科では高校までの数学の内容をしっかりマスターして最近の多方面への広がりを見せる数理科学に興味があり、計算だけではなく数学の論理的構造をじっくり学ぶこと、さまざまな事象に内在する本質を見ぬく洞察力を養成したい学生に対して、代数学、幾何学、解析学の基礎が身につくような学習プログラムを採用しています。また柔軟な思考力を養うために、意欲のある学生のために数学以外の理工系の科目も用意しています。
研究室の窓
問題解決のための数学的構成能力、論理的思考能力を培う。
人工知能(AI)、金融工学、統計的機械学習などに代表される新しい分野では、特に数学的思考に基づいて現象の本質を解析する能力や数理的定式化を行う能力が必要とされています。しかし、数学を知識として覚えるだけでは役に立ちません。数学科では、問題解決のために必要となる新しい数学を基礎から理解し、さまざまな分野で活用できるように、代数学、幾何学、解析学などの基礎を身に付けるための学習プログラムを用意しています。
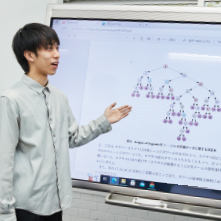

システム理工学部 数学科 2023年3月卒業
岡本 垂貴
Q. 特別研究で取り組んでいることを教えてください。
決定木と呼ばれる機械学習アルゴリズムを用いて、『League of Legends』というゲームの勝敗に影響する要素は何か、勝率を高めるにはどうすればよいかを分析しました。その結果、定石に沿ったプレイが勝率を高めることを再確認できました。
Q. 研究の展望を教えてください。
膨大なプレイデータを分析することで、4年間で培った数学の知識が世の中でどのように活用できるかを体感できました。卒業後はゲーム関連会社に勤めるので、この経験を生かしてよりユーザーが楽しめるゲーム作りに貢献したいと思います。
学びのキーワード
【代数・幾何・解析】
【解法発見の喜び】
【魅惑の定理との出合い】
代数学、幾何学、解析学、統計学など、純粋数学から応用数学まで、少人数クラスで数学の幅広い知識を修得できるような学習プログラムを採用しています。講義・演習・ゼミナールを通して、計算だけでなく数学の論理的構造をじっくり学び、さまざまな事象に内在する本質を見抜く洞察力を養成します。特に、ゼミナール形式の授業は全ての学年で受講するようになっており、少人数で教員との直接対話を通して数学の考え方を身に付けていくとともに、プレゼンテーション力やコミュニケーション力を磨いていきます。柔軟な思考力を養うために数学以外の理工系の科目も用意しています。
取得できる資格
所定単位を修得すると資格を取得できるもの
中学校教諭一種免許状〔数学〕 、高等学校教諭一種免許状〔数学〕 、司書、司書教諭、学芸員
申請することで資格を取得できるもの
測量士補
一定の実務経験を積むと資格を取得できるもの
測量士