マルコフ連鎖モンテカルロ法という理論を研究しています。これは、計算が困難な積分を近似的に解くための強力な手法です。現実に起こる事象は、多くの要素が絡み合って簡単には解けない場合が大半ですが、それを数学的に処理するには、正確性よりも実用性の高い近似値を早く見いだすことが重要です。AIや機械学習の基となるこの理論をより発展させて、新たな技術や理論の発見につなげたいと思います。

山﨑先生のゼミでは、必要な条件を満足させつつ最も適切な解を求める「最適化」の数学と、その方法としての数理計画法を研究します。私はその応用として、移動時に最短経路を探索する数学式を立て、それをPythonというプログラミング言語を用いたシミュレーションで検証しました。日常生活やビジネスで活用できる数学を学んだ経験を、教員になって生徒にも伝えたいと考えています。

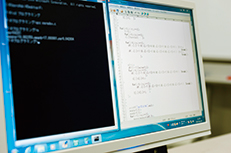
4年次前期に受けたコンピュータの授業が面白く、自分でもプログラムを作ってみたいと志願したところ、先生がコイン投げの不思議な現象に関する論文を紹介してくださいました。「コイン投げの試行列における2つのパターンAとBに関して、期待値を比べるとBがほうが早く出るはずなのに、確率を計算するとBが早く出る確率は1/2よりも小さくなる」という内容でした。この相容れない現象に興味をもち、検証に取り組みました。具体的には、確率論とプログラム言語を用いてシミュレーションする方法になります。プログラムは1文字でも誤入力があると、エラーが発生します。時には先生からアドバイスをいただきながら、一つずつ地道な修正作業を繰り返すことで、正確な統計的シミュレーションが完成。期待した結果が画面に表示されたときの喜びは、言葉で言い表せないほどです。卒業後はSE（システムエンジニア）として就職。これから必要となる知識や技術も貪欲に吸収していこうと思います。

卒業論文で取り組んだテーマは「シルベスターの問題」。「n個の点が一直線上にないとき、2点だけを通る直線が少なくとも1本は存在する」という内容です。高校と違って大学の数学は、数式だけでなく論理的な説明が必要となります。卒業論文の中間発表でも、どのような公理や定理に基づくのかを提示しながら証明。数式を書きながら説明し、研究室のメンバーからの質問にも答えます。教科書では省略されていた部分に気付かず進めていると先生からも「どうして、そうなるの」と鋭い指摘が。友人たちから「こんな考え方を用いては」などと助けられながら補いました。塾のアルバイトで教えていた中学生がこの問題に興味をもったため、図を描きながら説明したところ「わかった」という反応が。証明できたうれしさと、教え子にも伝わった充実感の両方を味わいました。今の研究室を選んだのは、藤岡先生の授業の進め方を見て尊敬していたからです。卒業後は中学教員として、先生から吸収した理解しやすい説明方法や、授業運営を実践したいです。

時間とともにランダムに変化していくものの動きをモデル化する、確率過程の理論を学んでいます。この理論は株価、為替などの変化を説明するだけでなく、化学、生物学など幅広い分野に応用できる基礎ツールだと聞き、興味をもって取り組んでいます。研究の基本は、海外の大学で使用されている教科書を原文で読み進めること。日本語の文献も参考にしながら内容をまとめ、週１回開講されるゼミで発表を行っています。他の学生や院生からの質問に答えることが、自分の研究に対する理解を深めるのに非常に役立ちます。私が４年次のとき、ドイツのドレスデン工科大学を中心とした数学科の学生交換プロジェクトに研究室が参加するようになりました。私もドレスデンでの3週間の研究交流を経験。ドイツや韓国の研究者とのディスカッションを通じ、数学は世界の共通言語だということを強く感じることができました。今後は研究テーマを絞りこみ、彼らと目的のある議論を進められるようになりたいと考えています。

「数理ファイナンス」とは、証券市場に関する金融や経済の問題を数理モデルを用いた数学的手法で議論する学問です。私は、特に市場のモデリングに用いられる確率微分方程式の解析について研究しています。現在は、毎週のゼミ発表を通じて、学部時代に学んだ測度論に基づく確率論やマルチンゲール理論などをベースに、確率微分方程式とそのファイナンスへ応用する手法について理解を深めているところです。この研究に興味をもったのは、3年次の夏に体験した銀行でのインターンシップで、普段学んでいる数学の知見が実務レベルでどう応用されているかを知ったのがきっかけです。
将来は、学部や大学院で学んだ数学の知識を生かして金融・保険業務の現場に携わることが目標。特に、保険・年金・リスク管理などの分野で活躍が期待される数理業務の専門家であるアクチュアリーに興味をもっていて、今後は自分の研究と両立させながらその資格取得にも挑戦したいと考えています。