諸科学分野で応用される、力学系理論と特異点論

専門分野について教えてください。

力学系理論と応用特異点論です。力学系理論というのは、ここでは物理で習う古典力学をイメージしてもらえたらと思います。天体の運動や分子の運動など複雑な動力学の法則性を、微分方程式を用いて数学的アプローチで解明しようという学問です。応用特異点論とは文字通り特異点論を数学内外に応用することを目的とする分野です。高校で勉強する1変数関数の極小点、極大点等の導関数がゼロになる点がここでいう特異点の例ですが、より一般の多変数の写像に対しても写像のヤコビ行列の階数が最大でなくなる点として特異点を定義することができます。最近は後者の応用特異点論を用い多目的最適化におけるパレート解全体の集合の数学的構造を研究しています。
　多目的最適化は、制約条件下で複数の目的関数を同時に最適化しようとするものですが、一般には一つの目的関数の値を改善しようとすると他の目的関数の値は改悪され、複数の目的関数を文字通り同時には最適化することができません。そこで多目的最適化においては、パレート解と呼ばれるある目的関数の値を改善するためには、少なくとも他の一つの目的関数の値を改悪せざるを得ないような解を考えます。パレート解は一般には複数あり得、状況に応じてパレート解の中から適切な解を選択する必要がありますが、適切な解を選び出すためには、可能な選択肢全体の集合であるパレート解全体の構造が分かっている必要があります。近年我々の研究により、パレート解集合全体の構造がどうなるかが、あるクラスの目的関数に対しては特異点論を使うことで解明されました。

特異点論を選ばれたきっかけは何だったのでしょうか。

特異点論の常套手段の一つに、幾何学的な対象に関する問題を代数の問題に帰着させて解くというものがありますが、一見とらえどころのない幾何学的対象に関する問題が、かっちりした代数の問題に帰着されるというところに興味を惹かれました。
　また、ひとたび代数の問題に帰着されれば、計算代数等の手法を用いて、その問題を計算機で解ける場合もあります。計算機の力を使って人の手では到底解けなかった問題を解けるようになることにも魅力を感じました。
　また、多目的最適化問題におけるパレート集合も、目的関数から定義される写像の特異点集合の部分集合となっており、写像の特異点集合を調べることにより、パレート集合の性質を調べることもできるなど、さまざまな応用があるのもこの研究を続けてきた理由です。そのテーマで企業と共同研究も行っています。

これまで研究テーマはどのように変わってきたのですか。

「自然は学問の垣根を知らない」というのは、1981年にアジアで初めてノーベル化学賞を受賞し、日本の理論化学の祖である福井謙一先生の言葉で、私が好きな言葉のうちの一つです。
　専門分野というものは、人が作った垣根のようなものだと思いますが、自然はそのような人の勝手な都合に忖度することは決してないため、専門分野にとらわれてしまうと、自然現象あるいは数学的現象の大局を見失う危険性があります。そのような理由から、あまり特定の専門分野にとらわれることなく、その時々で自分が重要だと考えることを研究してきました。
　ただ、研究テーマにも流行り廃りがあり、特に最近ではその変化が激しくなっています。変化が激しい時代だからこそ、できるだけ不変なものを求めたいという思いがあり、流行に流されず、堅実に一歩ずつ基盤を固めていけるような研究テーマを選んできました。

Dynamical system theory and singularity, which have many applications to various scientific fields

What is your area of expertise?

The area I study is dynamical systems theory and applied singularity theory. Dynamical systems theory is to elucidate dynamics of various things ranging from small molecules to celestial bodies through a mathematical approach using differential equations. Applied singularity theory aims to apply singularity theory to various scientific fields. Singularity can mean different things to different fields of science. In the current context, the simplest example of singularity is a stationary point of a function, which can be generalized to that of a mapping. Recently, I have been working on mathematical structures of Pareto sets and fronts in multi-objective optimization problems by using singularity theory.
　Multi-objective optimization is a field that attempts to optimize multiple objective functions simultaneously under certain constraints. However, in general, trying to optimize the value of one objective function results in a deterioration of the values of the other objective functions, and it is impossible to literally optimize multiple objective functions simultaneously. In multi-objective optimization, we therefore consider what is called the Pareto solution, which is the solution where the value of at least one other objective function must deteriorate in order to improve the value of a certain objective function. In general, there can be several Pareto solutions, and we need to select the appropriate solution from among the Pareto solutions depending on the situation. To do that appropriately, we need to know the overall structure of Pareto solutions. Our recent study elucidates the mathematical aspect of the overall structure of Pareto solutions for a certain class of multi-objective optimization problems.

What made you choose this field of research?

One of the usual practices in singularity theory is to reduce problems in geometry to those in algebra. I am interested in the fact that a problem on a seemingly elusive geometric object can be reduced to a solid algebraic problem by using singularity theory.
　Once a problem is reduced to an algebraic problem, it may be solved on a computer using methods such as computational algebra. I also find it fascinating to be able to use the power of computers to solve problems that could never be solved by human hands.
　The Pareto set in a multi-objective optimization problem is also a subset of the singularity set on the map defined by the objective function, and it is possible to investigate the properties of the Pareto set by examining the singularity set of the map. Another reason I have continued this research is that there are various applications. I am also conducting joint research with companies on this theme.

How has the research theme changed so far?

"Nature does not know the boundary of science." are the words of Professor Kenichi Fukui, who was the first Asian recipient of the Nobel Prize in Chemistry in 1981 and the founder of theoretical chemistry in Japan. This is one of my favorite words.
　Fields of specializations are boundaries created by people, We may miss big picture of natural or mathematical phenomena if we get caught in a specific field. For this reason, I have studied what I consider to be important from time to time, rather than focusing too much on a specific field.
　However, research themes also come in and out of fashion, and these changes are especially intense these days. I wish to seek something invariant because we are in an age of rapid change, and I have chosen research themes that do not follow trends and that can solidify the foundation.

社会課題解決に向けて、多目的最適化手法を応用

多目的最適化とは、どういった方法論でしょうか。

多目的最適化問題とは、例えばどこかの都市までできるだけ早くかつ安く行く交通手段を求める問題ですが、一般には早さと安さにはトレードオフの関係があり、飛行機で行く方が早く着くけど、電車で行く方が安いという状況はよくあると思います。このイメージが、多目的最適化の端的な問題です。この場合には、時間と経費という2つが目的関数となります。例えば電車、飛行機以外に自転車で行くことも考えられますが、自転車で行くと道中の宿泊費等を加味すると電車で行くよりも高くつき、かといって飛行機よりも時間がかかるので、自転車で行くというのはパレート解とはなり得ません。パレート解とはある意味トレードオフ、つまり一得一失を表すような曲線になっています。
　実際にどの交通手段で行くべきかは、その時の状況によって異なりますが、状況に応じて適切な解を選択するためには、可能な選択肢全体の集合であるパレート解全体の構造が分かっている必要があります。

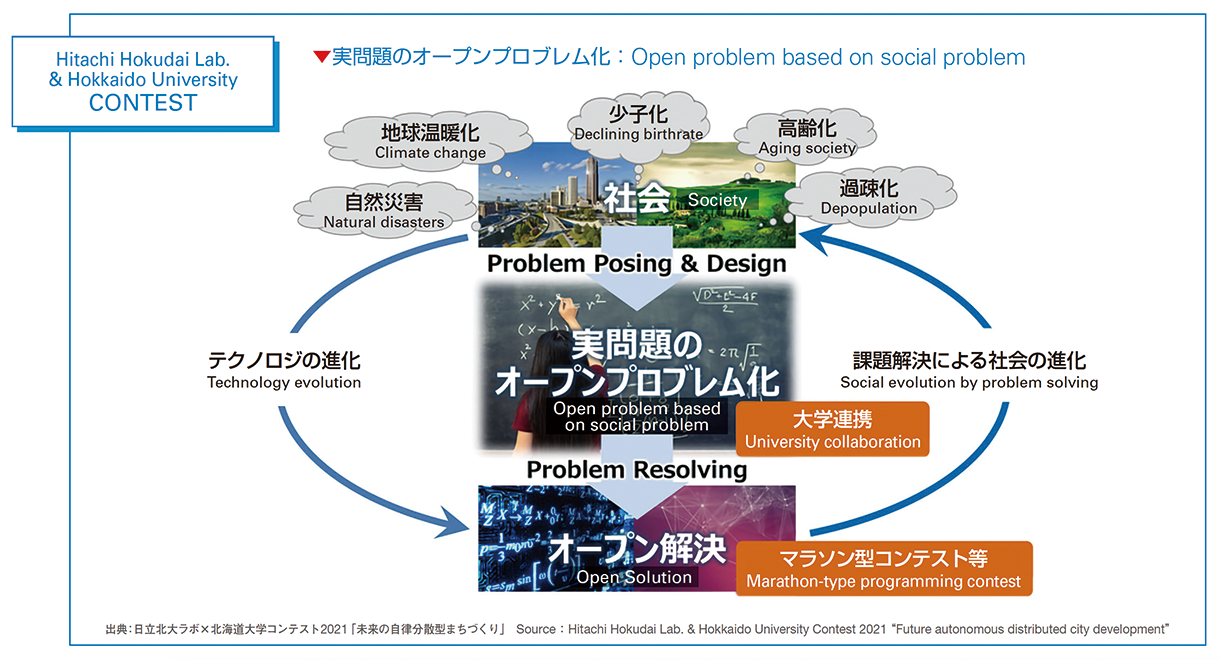
企業とはどのような共同研究をされているのでしょうか。

「Hitachi Hokudai Lab. & Hokkaido University Contest」は、日立製作所と北海道大学共催のプログラミングコンテストで、関西大学も問題作成等で協力しています。2020年度は国内外から1,700人の参加がありました。複雑化する社会課題解決に向けて、明確な評価基準とアルゴリズムの考案を目的としたコンテストで、これまで、アニーリングマシンの前処理技術に関する問題、買物支援サービスや地域エネルギーシステムの時空間最適化技術に関する問題等を出題しました。最適解を求めるアルゴリズムの問題ですが、その背景にあるのが、前述の多目的最適化です。
　コンテストを通じて考案されたアルゴリズムは、実応用に向けた検討を実施し、国際会議で研究成果を発表しています。2020年度は、優秀者と成果をまとめた論文「ナノグリッドネットワークで複数の電気自動車を使用することによる輸送と電力管理の多目的時空間最適化」を上梓しました。

Application of the multi-objective optimization method to solve social problems

What exactly is the methodology called multi-objective optimization?

A multi-objective optimization problem is, for example, a problem to find the mode of transportation to get to a city as quickly and cheaply as possible. In general, there is a trade-off relationship between speed and cheapness, and it is common to find that we arrive faster by plane but more cheaply if we take the train. In this case, the two objective functions are time and cost. For example, besides going by train or plane it is possible to go by bicycle, but if you go by bicycle, it is more expensive than going by train if you include the accommodation fee, etc. along the way. It also takes more time than going by plane, so going by bicycle cannot be a Pareto solution. A Pareto solution is in a sense a trade-off, a curve that expresses gaining something and losing something.
　Although which mode of transportation should actually be used depends on the situation at the time, we need to know the overall structure of the Pareto solutions, which are a set of all possible choices, in order to select the appropriate solution for the situation.

What kind of joint research are you conducting with corporations?

"Hitachi Hokudai Lab. & Hokkaido University Contest" is a programming contest co-sponsored by Hitachi, Ltd. and Hokkaido University. Kansai University also cooperates in creating the problems. In FY 2020, there were 1,700 participants from Japan and overseas. It is a contest that aims to devise clear evaluation criteria and algorithms for solving social issues that are becoming increasingly more complex, and so far we have set questions concerning pre-processing technologies for annealing machines, shopping support services, and spatio-temporal optimization technologies for regional energy systems, etc. They are problems of algorithms to derive the optimal solution, and what lies in the background is the multi-objective optimization described previously.
　The algorithms developed through the contest are examined for practical application, and research results are presented at international conferences. In FY 2020, we published a paper "Multi-objective Spatio-temporal Optimization of Transportation and Power Management by Using Multiple Electric Vehicles in Nanogrid Networks," which summarized the top performers and the outcomes.

最適な構造設計を構築するトポロジー最適化

今後の抱負をお聞かせください。

現在、トポロジー最適化の共同研究にも取り組んでいます。トポロジー最適化とは、与えられた制約のもと、ある目的関数を最大化あるいは最小化するような材料の密度分布を導き出す手法です。例えば、車体を重量の制約のもとその強度を最大化するなどの問題は典型的なトポロジー最適化の問題です。しかしながら、従来のトポロジー最適化の手法では、導き出された材料分布が、実際に作りやすいかどうかにはあまり注意が払われておらず、ものづくりへの応用は限定的なものでした。そこで我々は作りやすさを考慮したトポロジー最適化の手法「幾何学的特徴量に対する偏微分方程式系に基づく幾何学的特徴制約付きトポロジー最適化（積層造形における幾何学的特異点を考慮したオーバーハング制約法）」を提案し、2021年4月に日本機械学会賞（論文）を受賞しました。上の車体の例でも、強度だけではなく作りやすさ等も考慮すれば、トポロジー最適化の問題も多目的最適化の問題となりますので、多目的最適化の手法が応用できる可能性もあります。

関西大学に着任されて1年ですが、関西大学の印象を教えてください。

数学科が理工系学部の下に独立してあり、専門的な教育が展開されているという点が他の大学にないユニークさです。これが大学の一つの特色になっていると思います。また数学科の先生方は素晴らしい研究をされていますので、ぜひいろいろな先生方と共同研究をしたいと思っています。

最後に、学生の皆さんへのメッセージをお願いします。

近年は分野の流行り廃りが激しいです。例えば深層学習等、数十年前には見向きもされなかった技術が、計算機等の性能の向上とともに一躍注目されるようになりましたし、今後も量子コンピュータ等の新しい技術がどんどん出てくると期待されます。しかしながら、そのような変化の激しい時代であっても、それらの技術の基礎となる数学の体系は大きくは変化していません。大学では目先の役に立つ技術を習得するだけではなく、変化の激しい時代を生き抜くための知識をぜひ身に着けてください。

Topology optimization to construct the optimal structural design

What are your aspirations for the future?

I am currently engaged in joint research on topology optimization. Topology optimization is to optimize material distributions under certain constraints to maximize or minimize a certain objective function. For example, maximizing body stiffness of a car under a weight constraint is a typical problem in topology optimization. In the previous studies, manufacturability of optimum material distributions has not been taken into account and thus their application to the actual manufacture was limited. We proposed a method in topological optimization taking manufacturability of optimum material distributions into account in the paper "Topology optimization with geometrical feature constraints based on the partial differential equation system for geometrical features (Overhang constraints considering geometrical singularities in additive manufacturing)", which was awarded the Japan Society of Mechanical Engineers Medal for Outstanding Paper in April 2021. In the example of car design, by taking its manufacturability into account on top of body stiffness, its optimization problem becomes a multi-objective optimization problem.

It has been a year since you started working at Kansai University. Please tell us your impression of Kansai University.

The university is unique and different from others in that the Department of Mathematics is independent under the Faculty of Science and Engineering, and that specialized education is being developed. I think this is one of the characteristics of the university. Also, the professors at the mathematics department are wonderful, and I am hoping to do joint research with many of them.

Finally, can you give a message to the students?

In recent years, research fields come in and out of fashion rapidly. For example, technologies such as deep learning, which were unheard of a few decades ago, have suddenly gained attention as the performance of computers and other devices has improved, and new technology such as quantum computers is expected to emerge in the future. However, the foundation of mathematics underlying these technologies has not changed significantly even in this time of rapid changes. I hope you will not only acquire skills that are immediately useful, but also the knowledge to survive through this time of rapid changes at the university.